PI Algorithms and Decoding Gabidulin Codes
Transmission and Networking Technologies Lab
Prof. Jiun-Hung Yu
Transmission and Networking Technologies Lab
Prof. Jiun-Hung Yu
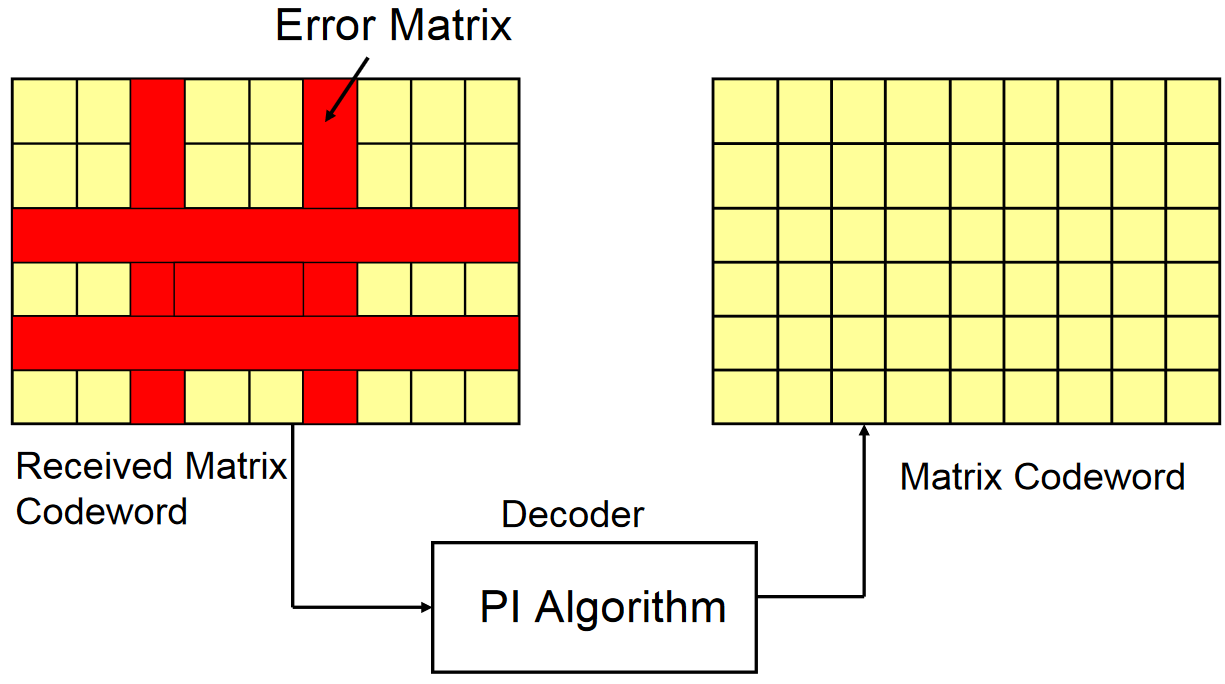
卡比杜林碼(Gabidulin codes)是最具代表性的矩陣碼,此碼可看成是矩陣版的里德所羅門碼(Reed-Solomon codes)。此矩陣碼可更正矩陣形式的錯誤,如上圖所示。只要錯誤矩陣(Error matrix)之Rank小於等於該碼的錯誤更正半徑(以rank度量),則可保證該矩陣錯誤可被更正。此矩陣碼可應用在網路編碼 (Network coding),使得在使用網路編碼提升網路封包(Packets)傳輸效率時也能同時確保傳送封包的正確性。針對該矩陣碼之解碼,我們提出適用於此矩陣碼 的PI 演算法,此演算法可快速從受到污染的矩陣碼中(其包含原始封包資料),找出矩陣形式的錯誤(含向量形式之錯誤)完成解碼,並恢復原始的封包資料。除了PI 演算法,我們也發展了整套基於PI演算法的代數解碼理論。
▶ J.-H. Yu and H.-A. Loeliger, "Simultaneous partial inverses and decoding interleaved Reed- Solomon codes," in IEEE Trans. Information Theory, vol. 64, no. 12, pp. 7511-7528, Dec. 2018. (Link)
▶ J.-H. Yu and H.-A. Loeliger, "Partial-inverse mod m(x) and reverse Berlekamp-Massey decoding," in IEEE Trans. Information Theory, vol. 62, no. 12, pp. 6737-6756, Dec. 2016. (Link)



