Topic:The Partial-inverse Approach to Reed-Solomon Codes, Gabidulin Codes, and the Related Algebraic Codes.
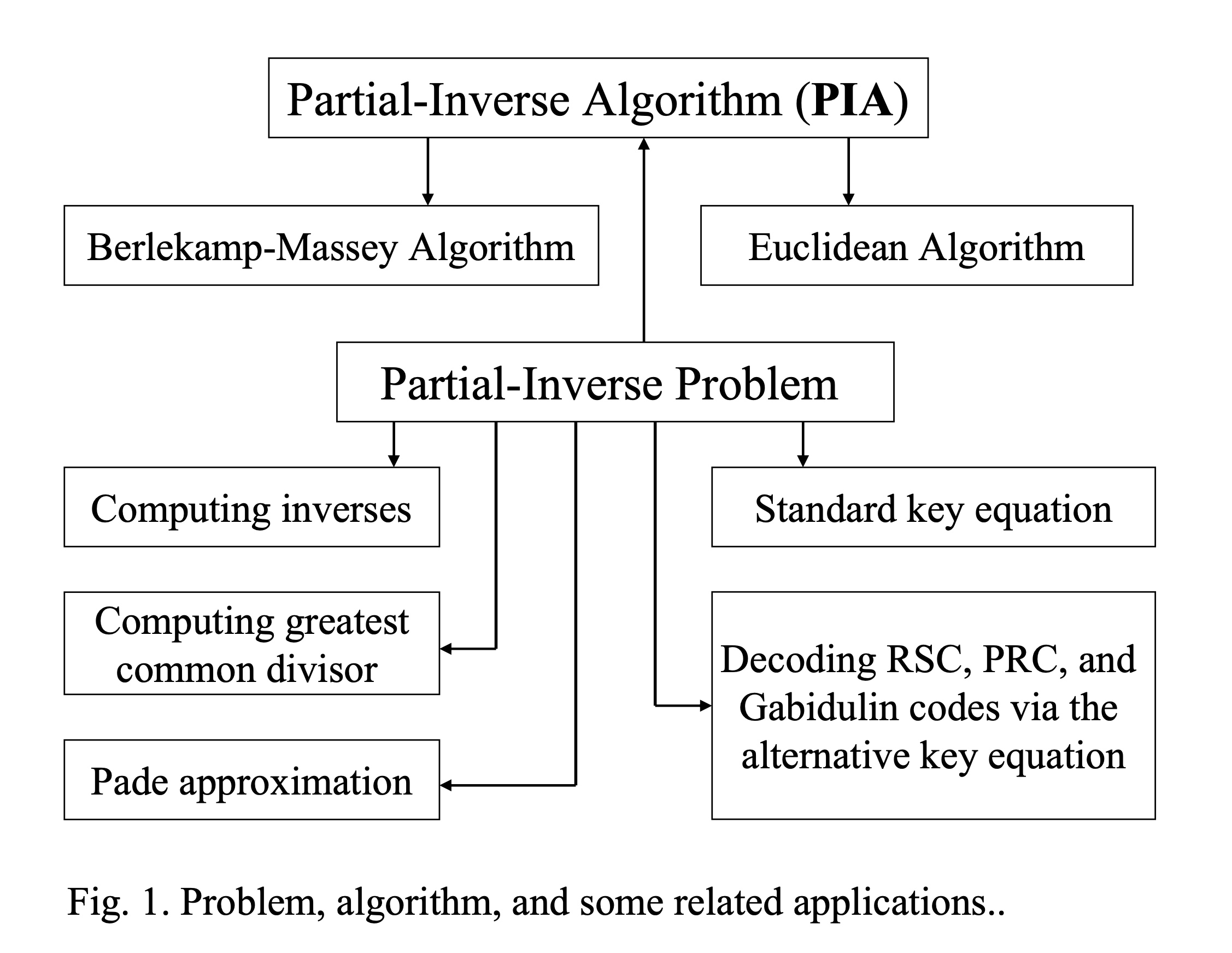
In the field of algebraic coding theory, we propose an approach based on the Partial-inverse (PI) Problem and PI Algorithm. This PI problem encapsulates several fundamental algebraic inquiries, including (1) solving the inverse element problem in algebraic rings, (2) computing the greatest common divisor of two polynomials, (3) polynomial division for quotient and remainder determination, (4) addressing Pade approximation problems, and (5) decoding Reed-Solomon codes and Gabidulin codes. We establish pertinent algebraic theorems and properties concerning the PI problem, providing a unified framework and perspective for relevant algebraic theories and decoding problems. Furthermore, our devised PI algorithm encompasses both the Berlekamp-Massey algorithm and the Euclidean algorithm, serving as a common parent algorithm for both and combining their respective advantages. The PI algorithm can solve problems that the Euclidean algorithm can solve, while operating similarly to the Berlekamp-Massey algorithm, exhibiting corresponding optimal decoding performance. It stands as a practical algorithm with feasible utilization. This PI Approach furnishes a comprehensive and efficient solution for Reed-Solomon codes, Interleaved Reed-Solomon codes, Gabidulin codes, and other related algebraic codes.
[1] J.-H. Yu and H.-A. Loeliger, ''The partial-Inverse approach to linearized polynomials and Gabidulin codes with applications to network coding,'' IEEE Transactions Information Theory, vol. 69, no. 6, pp. 3759–3774, June, 2023. (
Link)
[2] J.-H. Yu and H.-A. Loeliger, "Simultaneous partial inverses and decoding interleaved Reed-Solomon codes," IEEE Transactions Information Theory, vol. 64, no. 12, pp. 7511–7528, Dec., 2018. (
Link)
[3] J.-H. Yu and H.-A. Loeliger, "Partial-inverse mod m(x) and reverse Berlekamp-Massey decoding," IEEE Transactions Information Theory, vol. 62, no 12, pp. 6737–6756, Dec. 2016. (
Link)
---------------------------------------------------------------------------------------------------------------------------------------------------------------

Topic:A ML-MMSE receiver for millimeter wave user-equipment detection: beamforming, beamtracking, and data-symbols detection
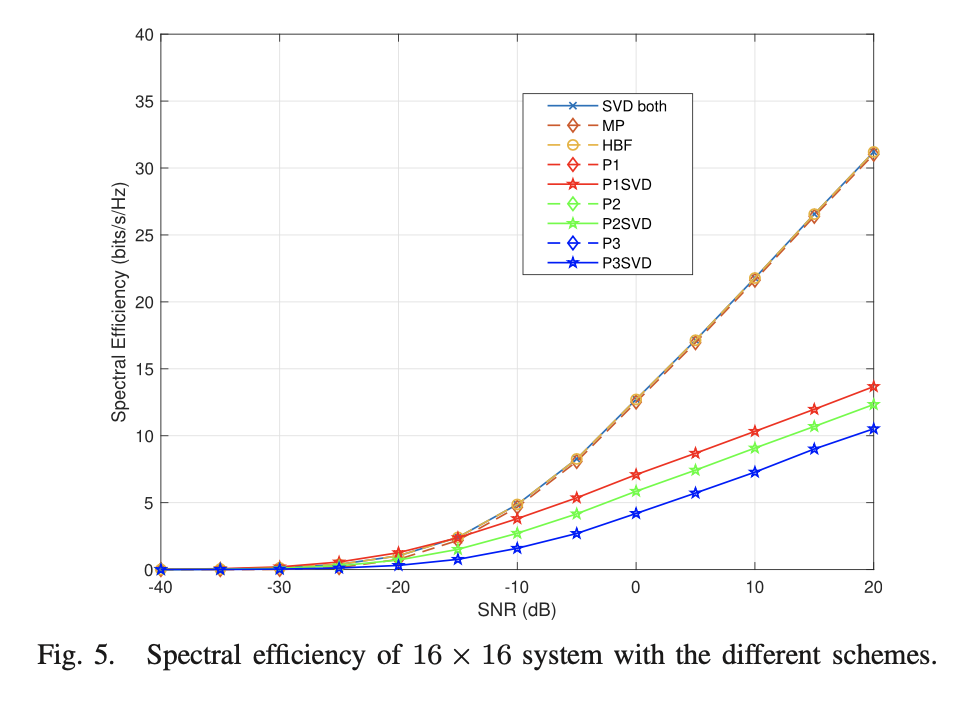
Our research delves into signal detection and data symbol reception in millimeter-wave communication systems, focusing on optimal receiver design for high directional channels. Specifically, we investigate beamforming, beam tracking, and data symbol detection under high directional millimeter-wave channels. Employing a hybrid beamforming architecture, we've devised a novel beam training algorithm that rapidly identifies the most reliable beams between base stations and user terminals for high directional communication. Notably, this algorithm boasts significantly low complexity, making it well-suited for mobile user terminal applications.
Additionally, we've developed a novel joint beam tracking and data symbol reception algorithm. This algorithm concurrently tracks and adjusts beam directions while receiving data symbols, addressing potential beam misalignment due to user terminal movement. Remarkably, this algorithm achieves beam auto-tracking and adjustment without the need for extra beam training symbols, effectively enhancing data throughput and maintaining high-quality millimeter-wave communication. Compared to existing literature, this represents the first algorithm with beam auto-tracking functionality that doesn't require extra beam training symbols.
Theoretical analyses and computer simulations demonstrate that the signal receiver developed in this research yields optimal baseband channels and achieves near-optimal spectral efficiency, as per theoretical benchmarks.
[1] J.-H. Yu, Z.-H. Yu, K.-L. Wu, T.-S. Lee, and Y. T. Su, ''A ML-MMSE receiver for millimeter wave user- equipment detection: beamforming, beamtracking, and data-symbols detection,'' IEEE Transactions Wireless Communications, vol. 20, no. 8, pp. 5301–5313, Aug., 2021. (
Link)



