余俊宏目前任職於國立陽明交通大學電機系電信工程研究所，專長為通訊系統接收機設計、編碼理論、以及統計訊號處理。余俊宏於2003年取得國立交通大學電信工程研究所碩士學位，2014年取得蘇黎世聯邦理工學院（ETH Zurich）電機工程博士學位。2003至2008期間，他任職於瑞昱半導體，擔任工程師與專案副理，起始第一代MIMO-OFDM系統（IEEE 802.11n）之無線基頻接收機設計，他所開發的核心訊號處理演算法已廣泛使用在瑞昱各種Wi-Fi相關產品中。2008至2017期間，他在瑞士 ETH Zurich ISI Lab進行研究工作，擔任RA、TA、與博士後研究員。余俊宏於2017年返國回母校電機系電信所服務，投入先進通訊技術與編碼理論領域之研究。回國後他參與科技部B5G以及6G大型專案計畫，發展新型毫米波波束成形與波束追蹤技術，與進行相關通訊主題研究。余教授也參與多項產學合作計畫，協助業界開發產品所需技術。

學歷:

o 國立交通大學    電信工程學系        學士
o 國立交通大學    電信工程研究所    碩士
o ETH Zurich    Electrical Engineering and Information Technology    博士

經歷:

o ETH Zurich    教學與研究助理，博士後研究       2008.10 ~ 2017.08
o 瑞昱半導體    工程師，資深工程師，專案副理    2003.10 ~ 2008.10

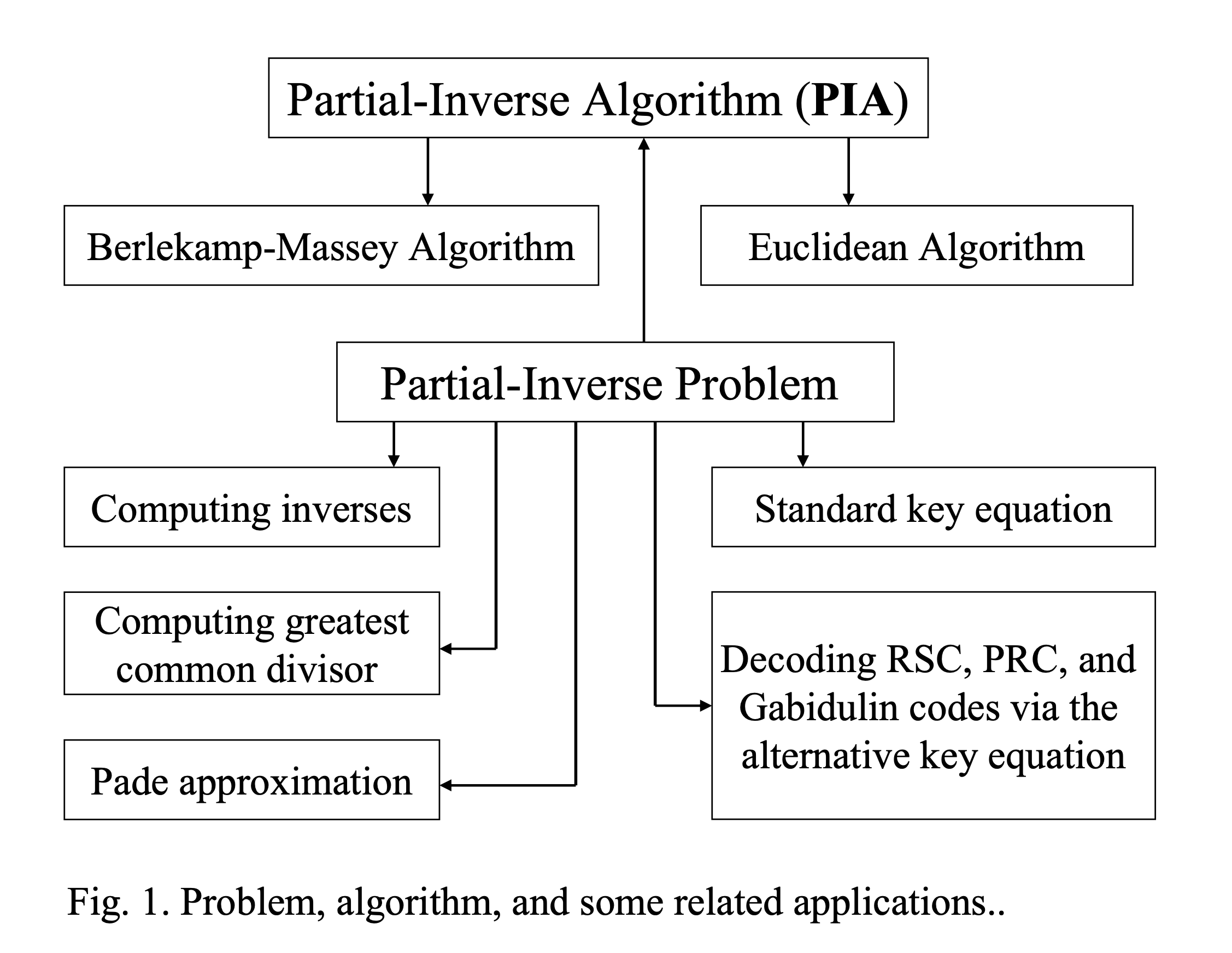
主題：The Partial-inverse Approach to Reed-Solomon Codes, Gabidulin Codes, and the Related Algebraic Codes. 

在代數碼領域，我們提出一套基於Partial-inverse (PI) Problem與PI Algorithm的Approach。此PI problem含括多個重要基礎代數問題，例如 (1)求解代數環中之反元素問題 、(2)計算兩多項式之最大公因數問題、(3)多項式除法求商與餘數問題、(4)Pade approximation問題、(5)解碼Reed-Solomon codes與Gabidulin codes問題。我們建立PI problem的相關代數定理與性質，為相關代數理論與解碼問題提供一個統一的框架與觀點。此外，我們提出的PI algorithm含括Berlekamp-Massey algorithm與Euclidean algorithm，可視為是兩者的Common parent algorithm，同時擁有兩者的優點。PI algorithm可解Euclidean algorithm可解之問題，並可以如同Berlekamp-Massey algorithm之運算方式進行運算，具對應之最佳解碼性能，是可實際使用的Practical algorithm。這套PI Approach為Reed-Solomon codes、Interleaved Reed-Solomon codes、Gabidulin codes以及其他相關代數碼提供一套完整並且有效的解決方案。

[1] J.-H. Yu and H.-A. Loeliger, ''The partial-Inverse approach to linearized polynomials and Gabidulin codes with applications to network coding,'' IEEE Transactions Information Theory, vol. 69, no. 6, pp. 3759–3774, June, 2023. (Link)
[2] J.-H. Yu and H.-A. Loeliger, "Simultaneous partial inverses and decoding interleaved Reed-Solomon codes," IEEE Transactions Information Theory, vol. 64, no. 12, pp. 7511–7528, Dec., 2018. (Link)
[3] J.-H. Yu and H.-A. Loeliger, "Partial-inverse mod m(x) and reverse Berlekamp-Massey decoding," IEEE Transactions Information Theory, vol. 62, no 12, pp. 6737–6756, Dec. 2016. (Link)
---------------------------------------------

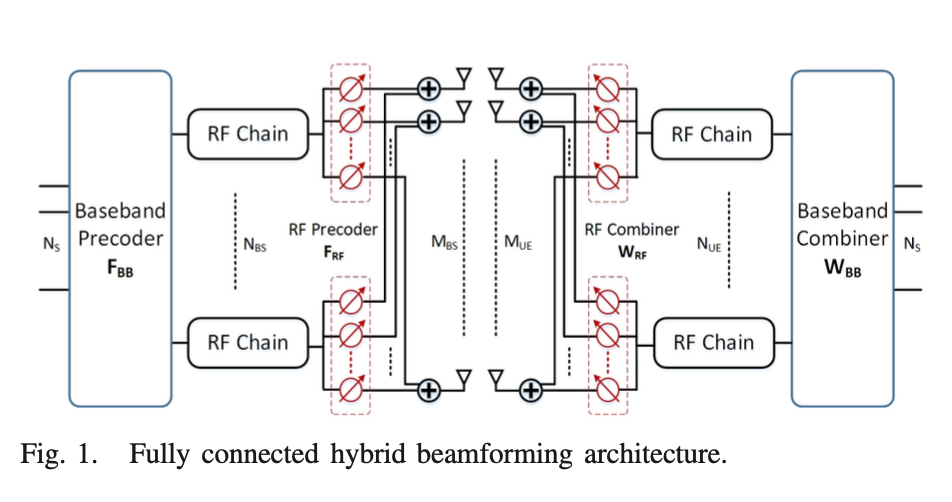
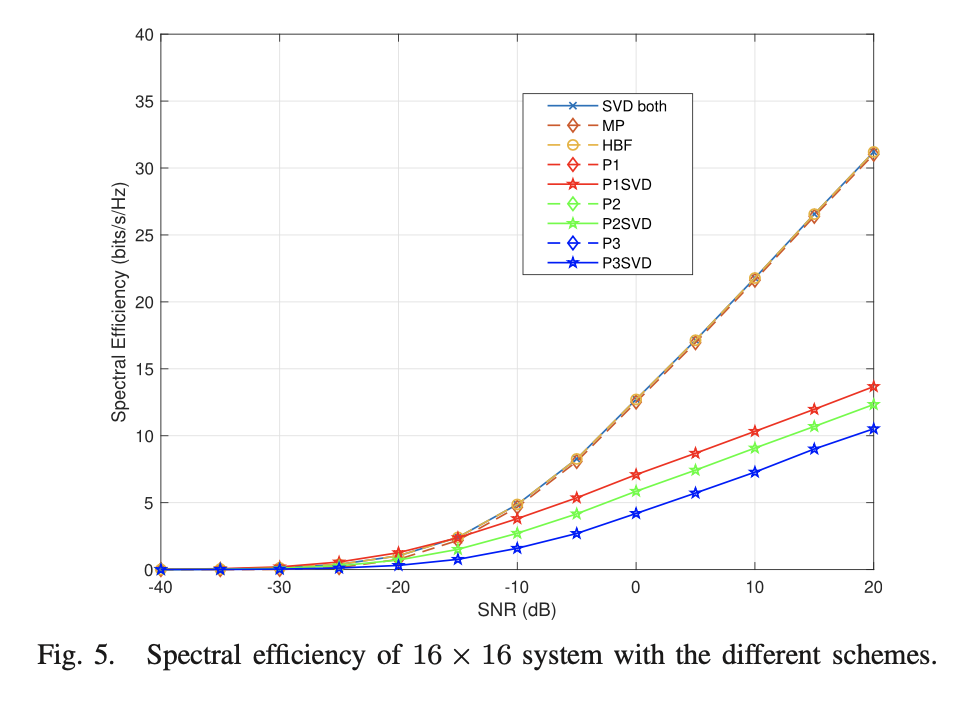
主題：A ML-MMSE receiver for millimeter wave user-equipment detection: beamforming, beamtracking, and data-symbols detection

本研究考慮毫米波通訊系統之訊號偵測以及資料符元接收問題，研究毫米波高指向通道下之波束成型、波束追蹤、與資料符元檢測之最佳接收機設計。使用混合式波束成型架構(Hybrid beamforming architecture)，我們設計了新型的波束訓練演算法，其可快速找到基站與用戶端最可靠的波束進行高指向通訊，此演算法有極低的複雜度，很適合手機用戶端使用。此外，我們也發展了新型的聯合式波束追蹤以及資料符元接收演算法，該演算法可以在接收資料符元時，同時追蹤調整波束方向以解決可能因用戶端移動所產生的波束偏移問題。該演算法無需使用額外的波束訓練符元便可完成波束自動追蹤調整，可有效提升資料傳輸之吞吐量，維持高品質毫米波通訊。與現行文獻相比，這是第一套具波束自動追蹤功能但無需使用額外波束訓練符元的演算法。理論分析與電腦模擬顯示，本研究開發的訊號接收機可以得到最佳的等效基頻通道，以及貼近理論上最佳的頻譜使用效益。

[1] J.-H. Yu, Z.-H. Yu, K.-L. Wu, T.-S. Lee, and Y. T. Su, ''A ML-MMSE receiver for millimeter wave user- equipment detection: beamforming, beamtracking, and data-symbols detection,'' IEEE Transactions Wireless Communications, vol. 20, no. 8, pp. 5301–5313, Aug., 2021. (Link)
 

●    Jiun-Hung Yu and H.-A. Loeliger, “The partial-inverse approach to linearized polynomials and Gabidulin codes with applications to network coding,” IEEE Trans. Inform. Theory, 2023, accepted for publication.
●    H. -C. Chang, Y. -C. Liu and Y. T. Su, "Detection of spatial-modulated signals in the presence of CSI uncertainty and spatially- and time-selective fading," pp. 107488-107504, IEEE Access, vol. 10, Oct. 2022.
●    T. C.-Y. Chang, P.-H. Chang, J.-J. Weng, I.-S. Lee and Y. T. Su, “Belief-propagation decoding of LDPC codes with variable node-centric dynamic schedules,” IEEE Trans. Commun. Vol. 69, no. 8. Pp. 5014-5027, Aug. 2021.
●    J.-H. Yu, Z-H. Yua, K.-L. Wu, T.-S. Lee and Y. T. Su “A ML-MMSE receiver for millimeter wave user-equipment detection: Beamforming, beamtracking, and data-symbols detection,” IEEE Trans. Wireless Comm. Vol. 20, no. 8, pp. 5301-5313, Aug. 2021.
●    W.-C. Chang and Y. T. Su, “Sparse Bayesian learning based tensor dictionary learning and signal recovery with application to MIMO channel estimation,” IEEE J. Select. Topics Sig. Proces. Vol. 15, no. 3, pp. 847-859, Apr. 2021.
●    J.-Y. Lai, W.-H. Wu and Yu T. Su, “Resource allocation and node placement in multi-hop heterogeneous integrated access-and-backhaul networks,” IEEE Access, Vol. 8, pp. 122937- 122958, Jul. 2020.
●     T. C.-Y. Chang, P.-H. Wang, and Y. T. Su, “Multi-stage bit-flipping decoding algorithms for LDPC codes,” IEEE Commun. Lett., Vol. 23, no. 9, pp. 1524 – 1528, Sep. 2019.
●    Jiun-Hung Yu and H.-A. Loeliger, "Simultaneous partial inverses and decoding interleaved Reed- Solomon codes," IEEE Trans. Information Theory. vol. 64, no 12, pp. 7511–7528, Dec. 2018.
●    T. C.-Y. Chang and Y. T. Su, “Adaptive group shuffled decoding for LDPC codes,” IEEE Commun. Lett., Vol. 21, no. 10, pp. 2118 – 2121, Oct. 2017.
●    C.-C. Cheng, H. Sari, S. Sezginer, and Y. T. Su, “New signal designs for enhanced spatial modulation,” IEEE Trans. Wireless Commun. Vol. 15, no. 11, pp.7766-7777, Nov. 2016.
●    Jiun-Hung Yu and H.-A. Loeliger, "Partial-inverse mod m(x) and reverse Berlekamp-Massey decoding," IEEE Trans. Information Theory, vol. 62, no. 12, pp. 6737–6756, Dec. 2016.
●    T. C.-Y. Chang and Y. T. Su, “Dynamic weighted bit-flipping decoding algorithms for LDPC codes,” IEEE Trans. Commun., Vol.63, no.11, pp.3950-3963, Nov. 2015.
●    C.-C. Cheng, S. Sezginer, H. Sari, and Y. T. Su, “Enhanced spatial modulation with multiple signal constellations,” IEEE Trans. Commun., Vol.63, no. 6, pp. 2237 – 2248, Jun. 2015.
●    Jiun-Hung Yu and Y. T. Su, "Pilot-assisted maximum likelihood frequency-offset estimation for OFDM systems," IEEE Trans. Communications, vol. 52, no. 11, pp. 1997–2008, Nov. 2004.

 

●    J.-H. Yu and H.-A. Loeliger, " Decoding Gabidulin codes via partial inverses of linearized polynomials," in Proc. IEEE Int. Symp. Inf. Theory (ISIT), Jun., 2019.
●    J.-H. Yu, "Decoding Reed-Solomon codes up to Sudan’s radius using simultaneous partial inverses," The 15th IEEE VTS Asia Pacific Wireless Commun. Symp., Hsinchu, Taiwan, Aug., 2018.
●    Y.-P. Yang, J.-H. Yu, and Y.-T. Su, ''Decoding time-domain Reed-Solomon codes with partial- inverse algorithm and generalized Horiguchi-Koetter interpolation,'' The 15th IEEE VTS Asia Pacific Wireless Commun. Symp., Hsinchi, Taiwan, Aug., 2018.
●    J.-H. Yu and H.-A. Loeliger, "Decoding of interleaved Reed-Solomon codes via simultaneous partial inverses," in Proc. IEEE Int. Symp. Inf. Theory (ISIT), Hong Kong, Jun. 2015.
●    J.-H. Yu and H.-A. Loeliger, "An algorithm for simultaneous partial inverses," in Proc. 52nd Annu. Allerton Conf. Commun. Control. Comput. Monticello, IL, USA, Oct. 2014.
●    J.-H. Yu and H.-A. Loeliger, "Reverse Berlekamp-Massey decoding," in Proc. IEEE Int. Symp. Inf. Theory (ISIT), Istanbul, Turkey, Jul. 2013.
●    J.-H. Yu and H.-A. Loeliger, J.-H. Yu and H.-A. Loeliger, "On irreducible polynomial codes," in Proc. IEEE Int. Symp. Inf. Theory (ISIT), Saint Petersburg, Russia, Jul./Aug. 2011., IEEE Int. Symp. Inf. Theory (ISIT), 2011, Saint Petersburg, Russia
●    J.-H. Yu and Y. T. Su, J.-H. Yu, J.-S. Jiang and Y.-T. Su, "ML solutions for resolving frequency ambiguity in OFDM systems," in Proc. IEEE Int. Conf. Wireless Networks, Commun. Mobile Comput, Hawaii, USA, Jun., 2005., IEEE Int. Conf. Wireless Networks, Commun. Mobile Comput, Nov. 2017, Hawaii, USA

●    J.-H. Yu, A partial-inverse approach to decoding Reed-Solomon codes and polynomial remainder codes, Konstanz , Germany: Hartung-Gorre, 2015, ISBN 978-3-86628-527-9

●    專利名稱: 基地臺與用戶設備進行連繫的方法, 專利編號 : TW I794920, 發明人名稱: 余俊宏, 發表日期 : 2023/03/01
●    專利名稱: 資料加密的錯誤偵測裝置及方法, 專利編號 : TW I804439, 發明人名稱: 余俊宏 等數位發明人, 發表日期 : 2023/06/01
●    專利名稱: 資料加密的錯誤偵測裝置, 專利編號 : TW I808902, 發明人名稱: 余俊宏 等數位發明人, 發表日期 : 2023/07/11​​​​​​
●    K.-Y. Yen, J.-H. Yu, D.-Z. Liu, and C.-Y. Chang, Wireless transmission apparatus and related wireless transmission method, patent number: 9136963, date of patent: September 15, 2015.
●    D.-Z. Liu, J.-H. Yu, and K.-Y Yen, Power saving apparatus and method of multiple-antenna receiver with variable rate, patent number: 8792575, date of patent: July 29, 2014.
●    C.-S. Lee, L.-W. Huang, J.-H. Yu, and S.-H. Kuo, Method and device for dynamic adjustment of network operating voltage, patent number: 7839152, date of patent: June 28, 2011.
●    J.-H. Yu, Searching method for maximum likelihood (ML) detection, patent number: 7920656, date of patent: April 5, 2011.